At the age of 11 or 12, children enter what famed psychologist Jean Piaget identified as the formal operational stage. While this represents the last of Piaget's stages of cognitive development, it's important to note that development continues in various aspects throughout life, including emotional, moral, and social dimensions. In the formal operational stage, children begin to think abstractly and can apply these abstract thoughts to problem-solving. It's during this stage that they also become acquainted with a process known as deductive reasoning.
Deductive reasoning is a process in which we conclude the world around us. It’s also one of the basic ideas introduced to students learning about logic and how to form an argument. Deductive reasoning can help us discover the truth, but as you’ll see in the video, sometimes this process is done so quickly because it’s obvious.
On this page, I will discuss deductive reasoning, how we use it in everyday life, and how it differs from inductive reasoning. Understanding deductive and inductive reasoning are essential building blocks for understanding how we make sense of the world and how we make decisions.
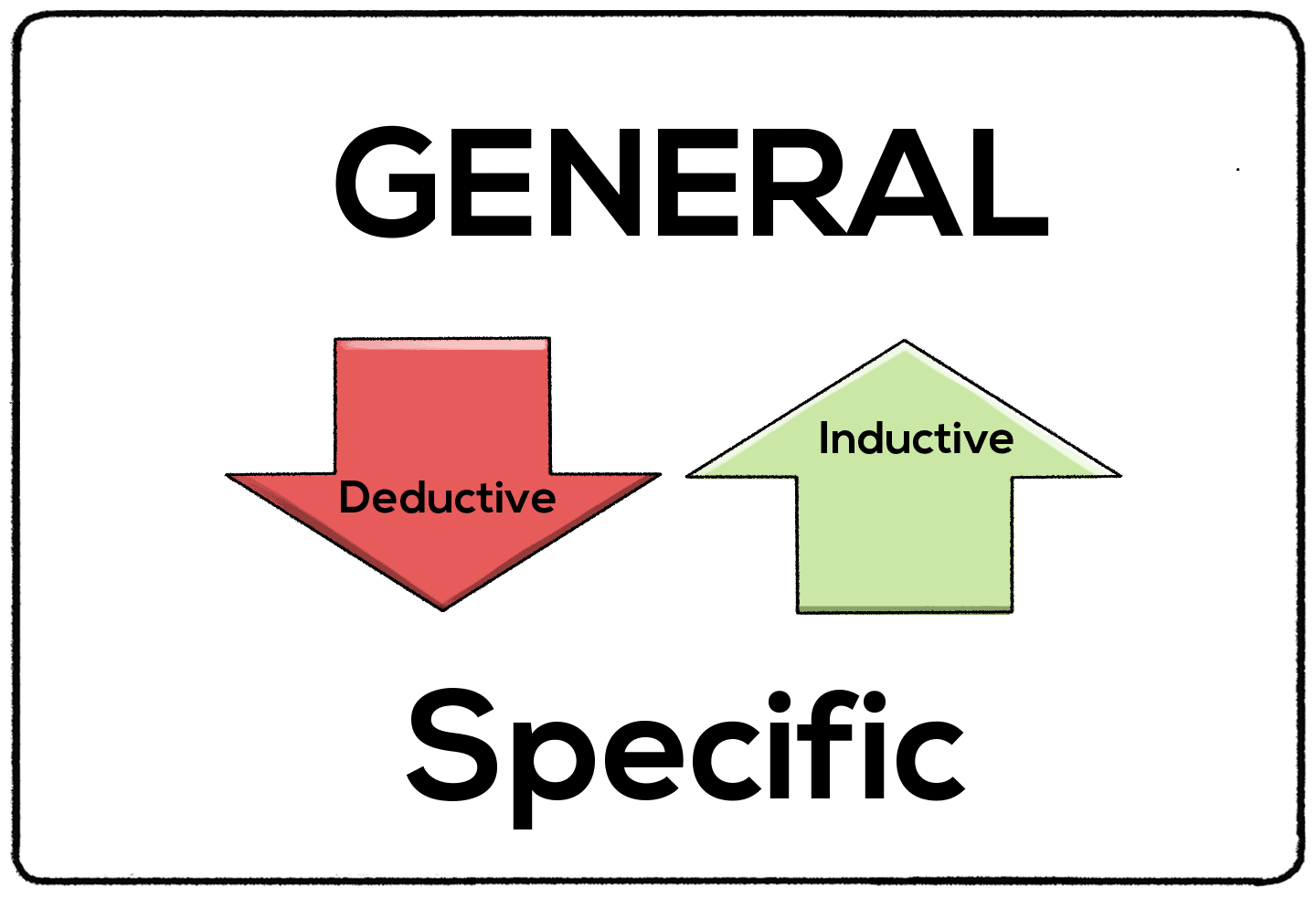
Top-Down vs. Bottom-Up Logic
When discussing reasoning and logic, two commonly used terms are "top-down" and "bottom-up." These terms refer to the direction or flow of information or reasoning.
- Top-Down Logic (Deductive Reasoning): This method begins with a general statement or hypothesis and examines the possibilities to reach a specific, logical conclusion. It's like starting from a broad perspective and narrowing it down. In essence, if the broader generalization is true, then the specific conclusion must also be proper.
- Bottom-Up Logic (Inductive Reasoning): This is the opposite of the top-down approach. It starts with specific observations and measures, begins to detect patterns and regularities, formulates some tentative hypotheses that we can explore, and finally develops some general conclusions or theories. Instead of starting with a broad generalization, we collect bits of data and form a general conclusion based on those observations.
Understanding Correlation in Reasoning
Another important concept to grasp when discussing reasoning is the idea of correlation. Correlation refers to a relationship or association between two or more variables. When two variables tend to change together consistently, they are said to be correlated.
- Correlation and Inductive Reasoning: Often, inductive reasoning involves observing correlations in the real world. For instance, we might observe that when one event happens, another event tends to follow. However, it's crucial to understand that correlation does not imply causation. Just because two variables change together doesn't mean one causes the other. Distinguishing between mere correlation and actual causation is vital for forming accurate conclusions based on observations.
For example, there might be a correlation between ice cream sales and the number of drowning incidents in a given area. While these two variables are correlated (both increase during the summertime), one does not cause the other. Instead, an external factor, like hotter weather, affects both variables.
What is Deductive Reasoning?
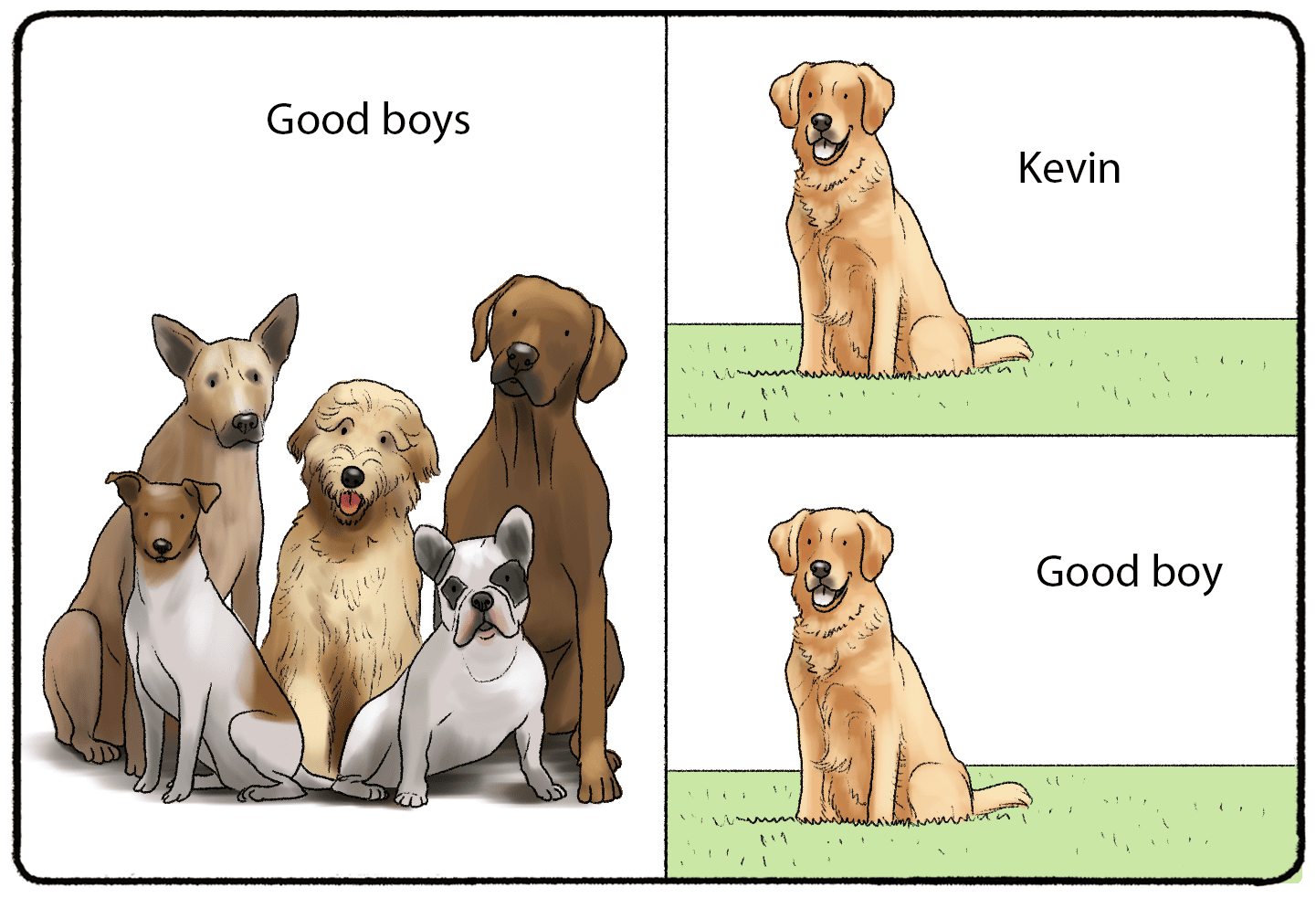
Deductive reasoning, or deduction, is the process of using a group of true premises to draw a conclusion that is also true. This is also known as “top-down logic” because it takes broad statements and uses them to create more narrow statements.
Here’s an example of deductive reasoning.
Premise A says that all dogs are good boys.
Premise B says that Kevin is a dog.
The conclusion that we draw from deductive reasoning says that Kevin is a good boy.
Of course, that example is silly, but it shows how we can use two ideas and deductive reasoning to form an argument or a statement. Other examples of premises like this include “all dogs are mammals” or “every human embryo is made from sperm and an egg.”
Premise A is typically a very broad and general statement. Premise B is a more narrow statement that relates to Premise A. The conclusion states a narrow truth relating to Premise A and Premise B.
Characteristics of deductive reasoning
To start the deductive reasoning process, you must use a statement that we all know to be true. If the statement is not true, or true sometimes, you may still be able to form a conclusion through induction. But to use deductive reasoning, that truth must be as solid as concrete.
It will also have to funnel down to make a more narrow conclusion through entailment. Premises A and B must be related so that Premise C can exist. Let’s go back to our example.
In both Premise A and Premise B, dogs are mentioned. Premise C grabs a conclusion from both premises in a logical, relevant way. When any of these parts of the deduction don’t follow the rules, problems may ensue.
Problems
The rules of deductive reasoning are airtight. If you’re not following them, you’re not using deductive reasoning. This may not change the validity of the premises or the conclusions you draw from your premises, but it does change whether or not it falls under the category of deductive reasoning.
If any of the following exist, you might end up coming to a false conclusion:
- False premises
- Lack of entailment
- A narrow truth
False Premises
Let’s go back to the idea that all dogs are good boys. In this case, one can unfortunately argue that not all dogs are good boys. This would automatically make the conclusion untrue. A conclusion is only considered the truth when the premises that precede it are true.
Notice here that we said that the conclusion is untrue. You may argue that Kevin is a good boy, even though not all dogs are. That means that the conclusion is valid. In philosophy, validity and truth are not the same thing.
So while some dogs are good boys, Kevin is a dog, and Kevin is a good boy, this is not a conclusion you can draw through deductive reasoning as ancient philosophers laid it out.
Lack of Entailment
Here’s another problem with deductive reasoning that we run into a lot. For a conclusion to be true, the premises that precede it directly support and lead to the conclusion.
Here’s an example of how failing to use this rule can create a weak conclusion. (Let’s go back to pretending that “all dogs are good boys” is a known fact.)
Premise A says that all dogs are good boys.
Premise B says that Kevin is a dog.
The conclusion drawn from this is that Kevin has blue eyes.
Kevin could very well have blue eyes, but just because the conclusion is valid doesn’t mean it is true because we have nothing to support the idea that Kevin’s eyes are blue.
Remember, you have to reach this conclusion through entailment. No premise has anything to do with the color of Kevin’s or any dog’s eyes. So we can’t come to that conclusion based on the premises given to us.
Narrow Truth
Think of all of the things that you know as true. Surprisingly, these broad and general facts are not easy to come by. And when they do, they seem too obvious to use in an example.
So deductive reasoning also seems very obvious, and outside of being the basis of forming an argument, it’s not useful in everyday life.
Let’s use another example of deductive reasoning, shall we?
Premise A says that all humans live on land.
Premise B says that Megan is a human.
The conclusion that you would get from deductive reasoning says that Megan lives on land.
Well, yeah. Duh. She’s a human, after all.
Deductive reasoning comes naturally to us. We do it without thinking. To figure out that a human lives on land or that a dog is a mammal is a quick process when you already know that all dogs are mammals and that all humans live on land.
However, due to the nature of deductive reasoning, you need those broad truths to conclude from. A more narrow truth won’t give you much to work with.
Example 1: All humans are mortal. Susan is a human. Susan is mortal.
This is a classic example of deductive reasoning. It starts with an entirely true statement - you can’t poke holes in it or argue against it. (Maybe in a few decades, you can, but not today!) The next statement is also true and ties into the first statement. The conclusion brings both statements together to create a statement that we have now proven is true.
Example 2: Marketing
In everyday life, we don’t always use deductive reasoning using the strict rules of traditional logic. Marketers, for example, may use deductive reasoning to make decisions about how they want to advertise their products to certain groups of customers.
They may use information from focus groups or surveys to create a profile of their products. Let’s say a company that makes cleaning products wants to target single women in their late 20s who are upper-middle-class. They collect information about the demographic and learn that upper-middle-class single women in their late 20s find more valuable products with natural ingredients and are “green.”
Premise 1 is that upper-middle-class women in their 20s find more value in products that have natural ingredients and are “green.”
Premise 2 is that the company’s target audience is upper-middle-class women in their 20s.
The marketers conclude that if they brand their products as “green” and highlight their natural ingredients, their target audience will find more value in their products.
Again, this doesn’t exactly fit the rules of “top-down logic.” Not every upper-middle-class woman particularly cares what is in their cleaning products. And not every upper-middle-class woman is in the company’s target audience. But this is often how we use deductive reasoning to conclude. These conclusions can still be very helpful, even if the conclusions aren’t 100% true.
Example 3: Deductive Reasoning in Math
Deductive reasoning is introduced in math classes to help students understand equations and create proofs. When math teachers discuss deductive reasoning, they usually talk about syllogisms. Syllogisms are a form of deductive reasoning that helps people discover the truth.
Here’s an example.
The sum of any triangle’s three angles is 180 degrees.
You are given a triangle to work with.
You can conclude that the sum of the triangle’s three angles is 180 degrees.
This conclusion will help you move forward when working with the triangle and discovering the length of each side or the measurement of each angle.
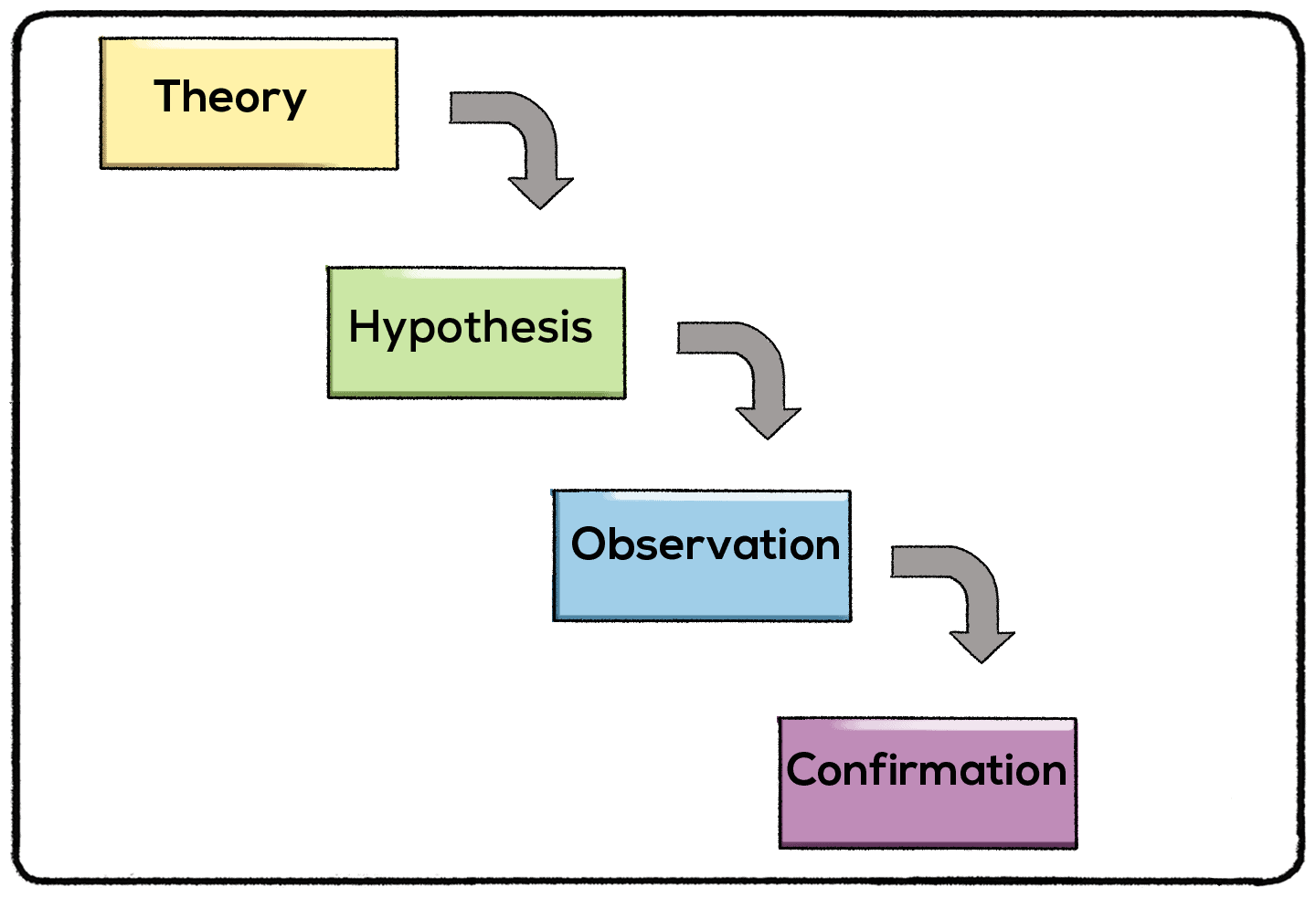
Example 4: Deductive Reasoning in Science
Deductions and induction are used to prove hypotheses and support the scientific method. Deduction requires us to examine how closely the premises and the conclusion are related. If the premises are backed by evidence and experiment, the conclusion will likely be true.
In the scientific method, scientists form a hypothesis. They then conduct experiments to see whether that hypothesis is true. With each experiment, they prove the strength of the premises and support their conclusion about whether or not their hypothesis is correct.
Without deductive reasoning, scientists may come to untrue conclusions or accept things that are likely as true things.
Deductive vs inductive reasoning
At the beginning of this video, I mentioned that child psychologist Jean Piaget theorized that children develop the skills of deductive reasoning around 11 or 12 years old. From then on, it’s not exactly something that we think about.
So we’re more likely to conclude things in the opposite direction. We use inductive reasoning to make sense of the world around us. We take a single experience or a few experiences from the past to conclude what might happen in the immediate future or indefinitely.
Inductive reasoning is more prevalent in our everyday lives because it requires a personal experience or a handful of facts. Getting down to the “truth,” especially if you are a philosopher or someone who is especially skilled in logic, is not always an easy thing to do. Plus, deductive reasoning doesn’t usually give us any incentive or confidence to take action. It just helps us build the world.
But I’ll talk more about inductive reasoning in my next video. I’ll break down what inductive reasoning is, the different types of inductive reasoning we use in everyday life, and the problems that come with inductive reasoning.
Test
Have you been listening? Let’s test your knowledge with a quick, three-question quiz on deductive reasoning.
First question:
Is deductive reasoning considered “top-down” or “bottom-up” logic?
Answer:
“Top-down logic.” It starts with broad truths and goes down to a more narrow conclusion. “Bottom-up logic” is called induction.
Second question:
What can interfere with deduction?
A: False premises
B: Lack of entailment
C: Narrow truth
D: All of the above
Answer:
All of the above! To arrive at the truth, you must provide true premises that logically lead to the conclusion. This means starting with a very broad truth and making your way down.
Last question: does this “count” as deductive reasoning?
Premise 1: All pigeons are birds.
Premise 2: John is a pigeon.
Conclusion: John is a bird.
Yes, it counts! All of the premises are true and contribute to the conclusion, which is also true.
